EdX

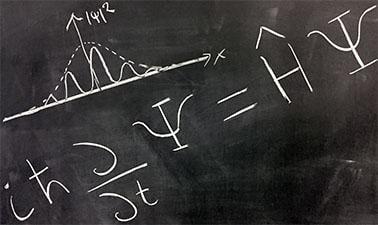
Quantum Mechanics: Quantum physics in 1D Potentials (edX)

Offered by MIT, MITx,
Quantum Mechanics: Quantum physics in 1D Potentials (edX)

Learn how to solve the Schrodinger equation for a particle moving in one-dimensional potentials relevant to physical applications. In this quantum physics course you will acquire concrete knowledge of quantum mechanics by learning to solve the Schrodinger equation for important classes of one-dimensional potentials.

Class Deals by MOOC List - Click here and see EdX's Active Discounts, Deals, and Promo Codes.

We study the associated energy eigenstates and bound states. The harmonic oscillator is solved using the differential equation as well as algebraically, using creation and annihilation operators. We discuss barrier penetration and the Ramsauer-Townsend effect.
This is the second course in a series which includes:

The series is based on MIT 8.04: Quantum Mechanics I. At MIT, 8.04 is the first of a three-course sequence in Quantum Mechanics, a cornerstone in the education of physics majors that prepares them for advanced and specialized studies in any field related to quantum physics. This online course follows the on-campus version and will be equally rigorous.
After completing the 8.04x series, you will be ready to tackle the Mastering Quantum Mechanics course series on edX, 8.05x.

What you'll learn

  • Solutions of the Schrodinger equation for one-dimensional potentials: the square well and the harmonic oscillator.
  • Algebraic solution of the harmonic oscillator.
  • Barrier penetration and the Ramsauer-Townsend effect.
Go to Class
MOOC List is learner-supported. When you buy through links on our site, we may earn an affiliate commission.

Related Courses

The Quantum Internet and Quantum Computers: How Will They Change the World? (edX) EdX
Delft University of Technology,DelftX

The Quantum Internet and Quantum Computers: How Will They Change the World? (edX)

Sci: Physics Science

Discover quantum computers and the quantum internet. Learn the principles and promises behind these developments and how they will impact our future. There is no doubt that quantum computers and the quantum internet will have a great impact on our world. But we don’t yet know quite how. As with traditional computers - we will only see the effects in the decades to come.This course will provide you with a basic understanding of quantum computing and the quantum internet. Together, we’ll peek into the fascinating world of quantum phenomena, such as qubits, superposition, and entanglement.

Self Paced
Self-Paced
Physics Quantum Quantum Computing
Details
Fundamentals of Transistors (edX) EdX
Purdue University,PurdueX

Fundamentals of Transistors (edX)

Engineering Eng: Electronics

This course develops a simple framework for understanding the essential physics of transistors, including modern nanoscale transistors. Important technology considerations and circuit applications are also discussed. The transistor has been called the greatest invention of the 20th century - it enabled the electronics systems that have shaped the world we live in. Today's nanotransistors are a high volume, high impact success of the nanotechnology revolution.

Feb 13th 2023
5-12 Weeks
Physics Digital Circuits Electrostatics
Details
The Radio Sky I: Science and Observations (edX) EdX
École Polytechnique Fédérale de Lausanne,EPFLx

The Radio Sky I: Science and Observations (edX)

Engineering Sci: Physics

Be captivated by the exotic objects that populate the Radio Sky and gain a solid understanding of their physics and the fundamental techniques we use to observe them. The serendipitous and unexpected discovery of radio emission from celestial objects opened up the possibility of studying a new and exciting view of the universe beyond the visible spectrum. Astronomers have been studying the cosmos in visible light since ancient Greece, but it is only in comparatively modern times that the universe beyond the visible spectrum has become accessible to us. In this course you will learn about the most important objects that emit in the radio regime, both within and beyond our own galaxy.

Self Paced
Self-Paced
Physics Photon Radio Sky
Details
Is this Physics or Magic? Learning Physics through Minds-on Science Demonstration (edX) EdX
National University of Singapore,NUS

Is this Physics or Magic? Learning Physics through Minds-on Science Demonstration (edX)

Sci: Physics

Is this MOOC an introduction to Physics or Magic? Here's calling all curious minds from every corner of the globe to join us to learn physics via science demonstrations which are exciting, visually appealing and thought provoking. In this MOOC, you'll get to witness how demonstrations can add reality and vividness to the process of concept formation, and pick up one or two scientific nuggets along the way.

Sep 5th 2023
5-12 Weeks
Physics Classical Mechanics Electrostatic Energy
Details
Advanced Transport Phenomena (edX) EdX
Delft University of Technology,DelftX

Advanced Transport Phenomena (edX)

Sci: Biology & Life Sciences Engineering

Learn how to tackle complex mass and heat transfer problems and apply the results in your own environment. How can you reduce the energy loss of your home? What is the underlying science of energy loss in pipes? Which heat and mass transfer problems do we have to tackle to make consumer products? In this engineering course, you will learn about the engineering principles that play an important role in all of these and more phenomena. You will learn about microbalances, radiation, convection, diffusion and more and their applications in everyday life.

Self Paced
Self-Paced
Physics Engineering Radiation
Details
Quantum Networking (edX) EdX
Purdue University,PurdueX

Quantum Networking (edX)

Sci: Physics Computer Science

Learn about the science and engineering of future quantum networks whose security is guaranteed by laws of quantum physics. Applying exotic quantum properties such as entanglement to every-day applications such as communication and computation reveals new dimensions of such applications. Quantum encoding and entanglement distribution provide means to establish fundamentally secure communication links for transfer of classical and quantum data.

Mar 27th 2023
5-12 Weeks
Physics Quantum Quantum Mechanics
Details