Ekaterina Amerik

Graduated from mathematical department of Moscow State University in 1992, went for graduate studies to the University of Leiden (the Netherlands), worked under the guidance of prof. A. Van de Ven. Ph. D obtained in spring 1997, title: «On the geometry of smooth hypersurfaces in projective space». Postdoc at Grenoble University (France) in 1997-1999. From september 1999, assistant professor at the University Paris-IX (Orsay, France); «habilitation» (a post-PhD degree existing in several european countries) obtained in 2007. From 2011 on, works at the mathemaical department of the Higher School of Economics, first as an assistant professor, then as a professor.

Sort options

Introduction to Galois Theory (Coursera)

Aug 1st 2022
Introduction to Galois Theory (Coursera)
Course Auditing
Coursera
Higher School of Economics - HSE University
Categories
Sci: Mathematics
Effort
Mixed
5-12 Weeks
1-4 Hours/Week
Languages
English
French
Portuguese
Russian
English
Spanish
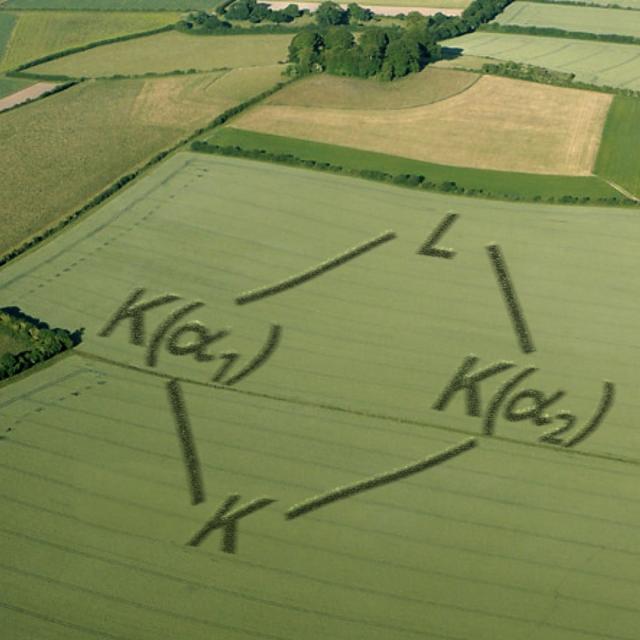
Introduction to Galois Theory (Coursera)
A very beautiful classical theory on field extensions of a certain type (Galois extensions) initiated by Galois in the 19th century. Explains, in particular, why it is not possible to solve an equation of degree 5 or more in the same way as we solve quadratic or cubic equations. [...]
Galois Theory
Quadratic Equations
Transcendentalism
Equations
Math
Polynomial
Mathematics
Coursera Plus
View more details
Aug 1st 2022
Course Auditing
Coursera
Higher School of Economics - HSE University
Sci: Mathematics
Mixed
5-12 Weeks
1-4 Hours/Week
41.00 EUR
English
French
Portuguese
Russian
English
Spanish